Willkommen auf den Seiten der maja.cloud
Lerne maja und Ihr Team kennen und wir zeigen Dir, wie einfach Cloud Computing sein kann.
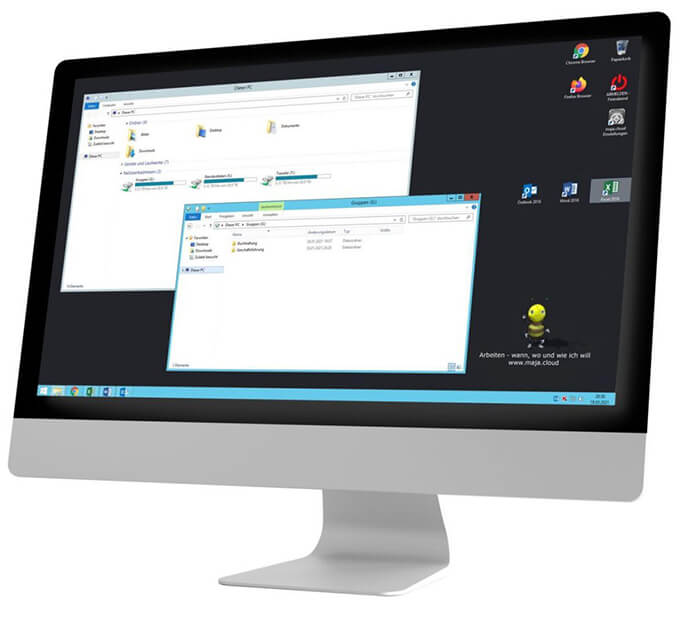
maja.cloud ist ein virtueller, unzerstörbarer Windows PC Arbeitsplatz, den Du überall hin mitnehmen kannst. Egal ob Büro, Praxis, Kanzlei, Home-Office oder von Unterwegs. Mit dem maja.cloud DESKTOP hast du überall sicheren Zugriff auf Deine Programme und Daten.
Und das geht kinderleicht!

Mit dem Laden des Videos akzeptieren Sie die Datenschutzerklärung von YouTube.
Mehr erfahren

Mit dem Laden des Videos akzeptieren Sie die Datenschutzerklärung von YouTube.
Mehr erfahren
SICHERHEIT ist wichtig beim Cloud Computing
Und damit alle Deine Daten sicher sind, haben wir alle unsere Rechenzentren ISO 27001 zertifizieren lassen. Darüber hinaus sorgen wir auch täglich für ein sehr hohes Maß an IT Sicherheit, zum Beispiel durch das einzigartige Mailbutler System, das Deinen Mailverkehr absichert. So kannst Du Dich also entspannt zurücklehnen und den IT Support unseren Experten überlassen.
Bei uns bist Du sicher!
Das sind deine Vorteile, wenn wir zusammen arbeiten:
- Verfügbarkeit
- Unabhängigkeit
- Flexibilität
Denn die maja.cloud ist mit Ihrer durchschnittlichen Verfügbarkeit von 99,998% immer für Dich da und stellt sicher, dass Dein Windows Arbeitsplatz immer funktioniert. 24 Stunden an 7 Tagen die Woche (24/7). Das gilt natürlich auch für die Programme auf Deinem virtuellen Arbeitsplatz.
Dank der Erreichbarkeit über das Internet bist Du Unabhängigkeit und es bleibt Deine Entscheidung von welchem Ort Du zugreifen möchtest. Büro oder Home-Office? Oder von unterwegs, aus dem Hotel oder von einem Freund aus. Mit der maja.cloud ist es egal ob Du an einem festen Ort arbeitest oder von unterwegs ein fremdes Gerät nutzen möchtest.
Auch welches Gerät Du nutzen möchtest steht Dir frei. Wir bieten Dir die Flexibilität das Gerät zu nutzen, das Du bevorzugst oder das Dir gerade zur Verfügung steht. Das kann Dein normaler Büro PC sein, ein Tablet oder sogar Smartphone. Natürlich kannst Du auch uneingeschränkt vom Apple MAC arbeiten und Deine Windows Programme bequem und einfach dort nutzen.
Daher prägen wir den Slogan:
Arbeiten: Wann , Wo und Wie ich will!

Lerne jetzt maja.cloud Office kennen
Maja.cloud OFFICE ist das Standard Office Paket in der Cloud. Mit dem Microsoft Office Paket in der maja.cloud hast Du die Office Produkte: Word, Excel, Outlook, etc. immer mit dabei. Auf Deinem virtuellen Arbeitsplatz stehen Dir diese Programme auf Knopfdruck zur Verfügung. Keine Installation oder lästiges Update mehr. Du hast immer die aktuellste Version der Microsoft Office Produkte zur Verfügung und kannst sofort loslegen mit der Büroarbeit.
Dein PC-Programm braucht Office um ordentlich zu funktionieren? Dann ist das maja.cloud OFFICE genau das richtige für Dich, denn Integrationsprobleme, Makro und Makro-Sicherheitsprobleme gehören damit der Vergangenheit an.
Zudem funktionieren alle Microsoft Office Programme sehr schnell und unabhängig von der Hardware Deines Gerätes. Die zentrale Datenablage der maja.cloud helfen Dir und Deinem Team den Überblick über Eure Dateien zu behalten und ermöglichen Euch eine strukturierte Ablage.

Produkt des Monats
Die WinWorker GmbH mit Sitz in Goch erleichtert Dir als Handwerker Deine Büroarbeit. WinWorker ist die Software für‘s Handwerk. Egal in welchem Gewerk Du tätig bist, mit WinWorker bekommst Du eine Software für alles.
- Angebots- und Rechnungserstellung
- Adressverwaltung
- Projektverwaltung
- Aufmaßerfassung
und vieles, vieles mehr ist in WinWorker bereits enthalten.
Vereinfache Deine Büroarbeit und sichere Dir über die maja.cloud auch gleich die Flexibilität und Verfügbarkeit. Damit Du unabhängig von Deinem Ort und Gerät Deiner Arbeit nachgehen kannst. Gerade zu Zeiten der Covid-19 Pandemie kannst Du Deine Mitarbeiter auch bequem ins Home Office setzen und stellst über die mobilen WinWorker Apps die Zusammenarbeit und Kommunikation sicher.

Dein unzerstörbarer, digitaler Büro Arbeitsplatz
Mit dem maja.cloud DESKTOP bekommst Du einen virtuellen Windows PC für Dein Büro. Der Desktop ist nicht nur schnell, dank der maja.cloud Technologie, er ist sogar unzerstörbar!
Häufige Installation und Updates von Windows und anderen Deiner Softwareprodukte machen den PC oft träge und sorgen für eine hohe Fehleranfälligkeit. Der maja.cloud Desktop ist dagegen immun! Auf unseren Servern wird Dein Windows Arbeitsplatz binnen weniger Sekunden immer wieder frisch zusammengestellt. Genau, Du hast richtig gelesen. Wir tragen keine Altlasten mit herum die Dich ausbremsen oder Fehler die Dich an Deiner eigentlichen Arbeit hindern. Mit jeder Anmeldung an Deinem maja.cloud DESKTOP bekommst Du ein frisches und vor allem schnelles System.
Dabei funktioniert Dein Desktop natürlich jedes Mal ohne Einschränkungen und auch all Deine Fachsoftware ist nach wenigen Sekunden einsatzbereit. Auch wenn mal etwas nicht funktioniert kannst Du dies durch einfache Neuanmeldung oder unser SmartRepair binnen weniger Sekunden selbst wieder reparieren.
Damit haben wir den Windows-PC-Arbeitsplatz unzerstörbar gemacht!